🌳 AVL 트리(Adelson-Velsky and Landis Tree)란?
AVL 트리는 이진 탐색 트리(Binary Search Tree, BST)의 일종으로,
트리의 균형을 유지하여 탐색, 삽입, 삭제 연산을 O(log n) 시간 복잡도로 보장하는 자기 균형 이진 탐색 트리다.
특징
- 균형 인수(Balance Factor, BF)
- 어떤 노드의 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
- 가능한 값: -1, 0, 1
- BF = 2 또는 -2가 되면 불균형 → 회전(Rotation) 필요
- 자동 균형 유지
- 삽입/삭제 시 불균형 발생 → 회전 연산으로 균형 유지
- 탐색, 삽입, 삭제 모두 O(log n)
여기서 주목할 점은 균형을 유지하기위해 하는 회전 연산이다.
근데 왜 균형을 유지해야할까? 얘도 어차피 이진트리 아닌가? 라고 생각이 들수도 있다.
하지만 이진트리에 값을 넣다보면 아래의 예처럼 한쪽으로 치우지는 경우가 생긴다
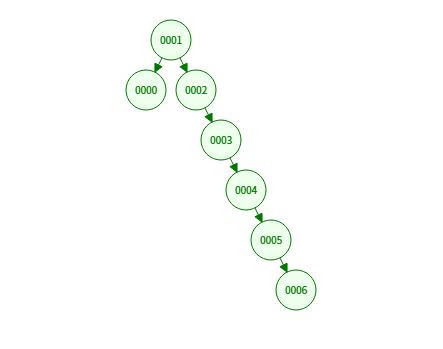
이러면 분기로 나뉘어 정보의 탐색이 빨라진다는 이진트리의 장점이 없어지게 된다.
그래서 나온게 트리의 높이를 삽입할때마다 조절해 균형을 맞추는 자기 균형 이진 트리이다.
얼마나 효율적으로 균형을 맞추는지가 자기 균형 이진 트리에서 재밌게 볼 수 있는 점일 것 같다.
하여튼 avl 트리는 이러한 문제를 방지하기 위해 한쪽이 다른쪽에 비해 높이가 2 이상 차이나면 트리의 구조를 회전을 통해 수정해준다.
avl 트리는 4가지 회전을 통해 불균형을 해결한다.
1. LL회전 (단순 오른쪽 회전, Right Rotation)
- 왼쪽-왼쪽(Left-Left) 불균형 발생 시 사용
- 왼쪽 자식이 다시 왼쪽 자식을 갖는 경우
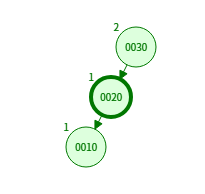
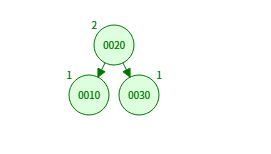
30을 오른쪽으로 회전 → 20이 루트가 됨
2. RR 회전 (단순 왼쪽 회전, Left Rotation)
- 오른쪽-오른쪽(Right-Right) 불균형 발생 시 사용
- 오른쪽 자식이 다시 오른쪽 자식을 갖는 경우
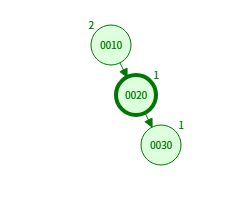
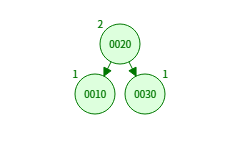
10을 왼쪽으로 회전 → 20이 루트가 됨
3. LR 회전 (좌-우 회전, Left-Right Rotation)
- 왼쪽-오른쪽(Left-Right) 불균형 발생 시 사용
- 왼쪽 자식의 오른쪽 서브트리가 불균형을 일으킨 경우
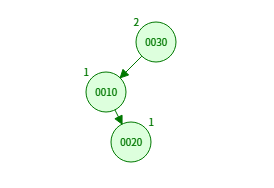
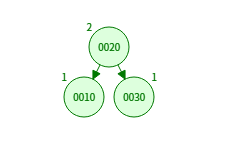
왼쪽 자식(10)을 왼쪽 회전(RR)
부모 노드(30)를 오른쪽 회전(LL)
4. RL 회전 (우-좌 회전, Right-Left Rotation)
- 오른쪽-왼쪽(Right-Left) 불균형 발생 시 사용
- 오른쪽 자식의 왼쪽 서브트리가 불균형을 일으킨 경우
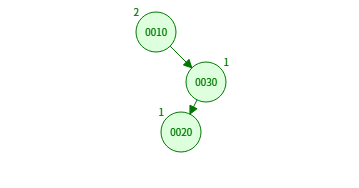
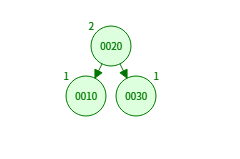
오른쪽 자식(30)을 오른쪽 회전(LL)
부모 노드(10)를 왼쪽 회전(RR)
구현 코드 GUI
실행환경
java 11 이상의 intellij
새프로젝트생성 -> 왼쪽 제너레이터 밑에 javaFX로 생성 후 아래 코드를 실행
구현시 주의점
기본적으로 입력은 이진트리와 비슷하지만 각 노드에 균형인수가 추가되었다.
그리고 삽입과 삭제 시 회전 조건이 달라지는 점!
삽입은 항상 새로운 노드가 추가되기 때문에 한쪽으로만 무거워짐 → 불균형이 단방향으로 발생
삭제는 노드 제거로 인해 트리가 양방향으로 불균형해질 수 있음.
삭제로 인해 왼쪽, 오른쪽 서브트리 모두 불균형 발생 가능.
삭제가 좀 복잡하다 삭제시에 균형인수를 잘 확인할 필요가 있따.
package com.example.demo;
import javafx.application.Application;
import javafx.geometry.Pos;
import javafx.scene.Scene;
import javafx.scene.canvas.Canvas;
import javafx.scene.canvas.GraphicsContext;
import javafx.scene.control.Button;
import javafx.scene.control.TextField;
import javafx.scene.layout.BorderPane;
import javafx.scene.layout.HBox;
import javafx.scene.paint.Color;
import javafx.stage.Stage;
public class HelloApplication extends Application {
private Avl root; // 트리의 루트 노드
private Canvas canvas;
public static void main(String[] args) {
launch(args);
}
@Override
public void start(Stage primaryStage) {
// 캔버스 생성
canvas = new Canvas(800, 600);
// 입력 필드 및 버튼 생성
TextField inputField = new TextField();
inputField.setPromptText("숫자 입력");
Button insertButton = new Button("삽입");
Button deleteButton = new Button("삭제");
// 버튼 이벤트
insertButton.setOnAction(e -> {
try {
int value = Integer.parseInt(inputField.getText());
root = insert(root, value);
drawTree(); // 트리 그리기
inputField.clear();
} catch (NumberFormatException ex) {
inputField.setText("숫자만 입력");
}
});
deleteButton.setOnAction(e -> {
try {
int value = Integer.parseInt(inputField.getText());
root = delete(root, value);
drawTree(); // 트리 그리기
inputField.clear();
} catch (NumberFormatException ex) {
inputField.setText("숫자만 입력");
}
});
// 레이아웃 구성
HBox controls = new HBox(10, inputField, insertButton, deleteButton);
controls.setAlignment(Pos.CENTER);
BorderPane rootPane = new BorderPane();
rootPane.setTop(controls);
rootPane.setCenter(canvas);
Scene scene = new Scene(rootPane, 800, 600);
primaryStage.setTitle("이진 탐색 트리 시각화");
primaryStage.setScene(scene);
primaryStage.show();
}
// 트리 그리기
private void drawTree() {
GraphicsContext gc = canvas.getGraphicsContext2D();
gc.clearRect(0, 0, canvas.getWidth(), canvas.getHeight());
drawNode(gc, root, canvas.getWidth() / 2, 50, canvas.getWidth() / 4);
}
// 노드 및 연결선 그리기
private void drawNode(GraphicsContext gc, Avl node, double x, double y, double offset) {
if (node == null) return;
gc.setFill(Color.LIGHTBLUE);
gc.fillOval(x - 15, y - 15, 30, 30);
gc.setFill(Color.BLACK);
gc.strokeOval(x - 15, y - 15, 30, 30);
gc.fillText(String.valueOf(node.value), x - 5, y + 5);
if (node.left != null) {
gc.strokeLine(x, y, x - offset, y + 50);
drawNode(gc, node.left, x - offset, y + 50, offset / 2);
}
if (node.right != null) {
gc.strokeLine(x, y, x + offset, y + 50);
drawNode(gc, node.right, x + offset, y + 50, offset / 2);
}
}
// avl tree에 삽입
public Avl insert(Avl node, int value) {
if (node == null) {
return new Avl(value);
}
if (value < node.value) {
node.left = insert(node.left, value);
} else if (value > node.value) {
node.right = insert(node.right, value);
} else {
// 중복 값 허용 X -> 그대로 반환
return node;
}
// 서브트리 높이 업데이트
node.left_size = getHeight(node.left);
node.right_size = getHeight(node.right);
// 균형 인수 계산
int balance = node.left_size - node.right_size;
// 회전(Rotation)으로 균형 조정
// LL 회전
if (balance > 1 && value < node.left.value) {
return rightRotate(node);
}
// RR 회전
if (balance < -1 && value > node.right.value) {
return leftRotate(node);
}
// LR 회전
if (balance > 1 && value > node.left.value) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RL 회전
if (balance < -1 && value < node.right.value) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 균형 상태 -> 그대로 반환
return node;
}
// avl tree에서 삭제
public Avl delete(Avl node, int value) {
if (node == null) {
return null;
}
if (value < node.value) {
node.left = delete(node.left, value);
} else if (value > node.value) {
node.right = delete(node.right, value);
} else {
// 삭제할 노드를 찾음
// 자식이 없거나 한 개일 때
if (node.left == null || node.right == null) {
Avl temp = (node.left != null) ? node.left : node.right;
// 자식이 없는 경우
if (temp == null) {
node = null;
} else { // 자식이 하나인 경우
node = temp;
}
} else {
// 자식이 두 개인 경우 -> 오른쪽 서브트리에서 최소값 찾기
Avl successor = getMinValueNode(node.right);
// 후계자의 값을 복사
node.value = successor.value;
// 후계자 노드 삭제
node.right = delete(node.right, successor.value);
}
}
// 노드가 null이면 그대로 반환
if (node == null) {
return null;
}
// 서브트리 높이 업데이트
node.left_size = getHeight(node.left);
node.right_size = getHeight(node.right);
// 균형 인수(Balance Factor) 계산
int balance = node.left_size - node.right_size;
// 불균형 해결 (회전)
// LL 회전
if (balance > 1 && getBalance(node.left) >= 0) {
return rightRotate(node);
}
// LR 회전
if (balance > 1 && getBalance(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RR 회전
if (balance < -1 && getBalance(node.right) <= 0) {
return leftRotate(node);
}
// RL 회전
if (balance < -1 && getBalance(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
private Avl getMinValueNode(Avl node) {
Avl current = node;
// 가장 왼쪽 노드 탐색
while (current.left != null) {
current = current.left;
}
return current;
}
private int getBalance(Avl node) {
if (node == null) return 0;
return getHeight(node.left) - getHeight(node.right);
}
// 최소값 찾기
public int getHeight(Avl node) {
if (node == null) return 0;
return 1 + Math.max(node.left_size, node.right_size);
}
// 오른쪽회전 - LL
private Avl rightRotate(Avl y) {
Avl x = y.left;
Avl T2 = x.right;
// 회전
x.right = y;
y.left = T2;
// 높이 업데이트
y.left_size = getHeight(y.left);
y.right_size = getHeight(y.right);
x.left_size = getHeight(x.left);
x.right_size = getHeight(x.right);
return x;
}
// 왼쪽회전 - RR
private Avl leftRotate(Avl x) {
Avl y = x.right;
Avl T2 = y.left;
// 회전
y.left = x;
x.right = T2;
// 높이 업데이트
x.left_size = getHeight(x.left);
x.right_size = getHeight(x.right);
y.left_size = getHeight(y.left);
y.right_size = getHeight(y.right);
return y;
}
// Avl 노드 클래스
public class Avl {
int value;
int left_size;
int right_size;
Avl left;
Avl right;
public Avl(int value) {
this.value = value;
this.left = null;
this.right = null;
this.left_size = 0;
this.right_size = 0;
}
}
}
'알고리즘공부 > 자료구조' 카테고리의 다른 글
| [자료구조] 트라이 (trie) (0) | 2025.01.20 |
|---|---|
| [자료구조] 트리순회 (전위, 중위, 후위) (0) | 2025.01.20 |
| [자료구조] 이진트리 (0) | 2025.01.17 |
| [자료구조] B+ tree (0) | 2025.01.17 |
| [자료구조] LinkedList (0) | 2025.01.16 |


