정렬이란??
일련의 데이터들을 정해진 규칙을 따라 순서대로 나열하는 것
정해진 규칙이란건 오름차순, 내림차순, 알파벳순서, 문자열의 길이 등 다양한 것이 될 수 있다.
정렬의 종류
1. 선택 정렬 (Selection Sort)
- 제자리 정렬 알고리즘의 하나
- 입력 배열 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법
- 시간 복잡도 O(n^2) 공간 복잡도 O(1)
정렬 과정
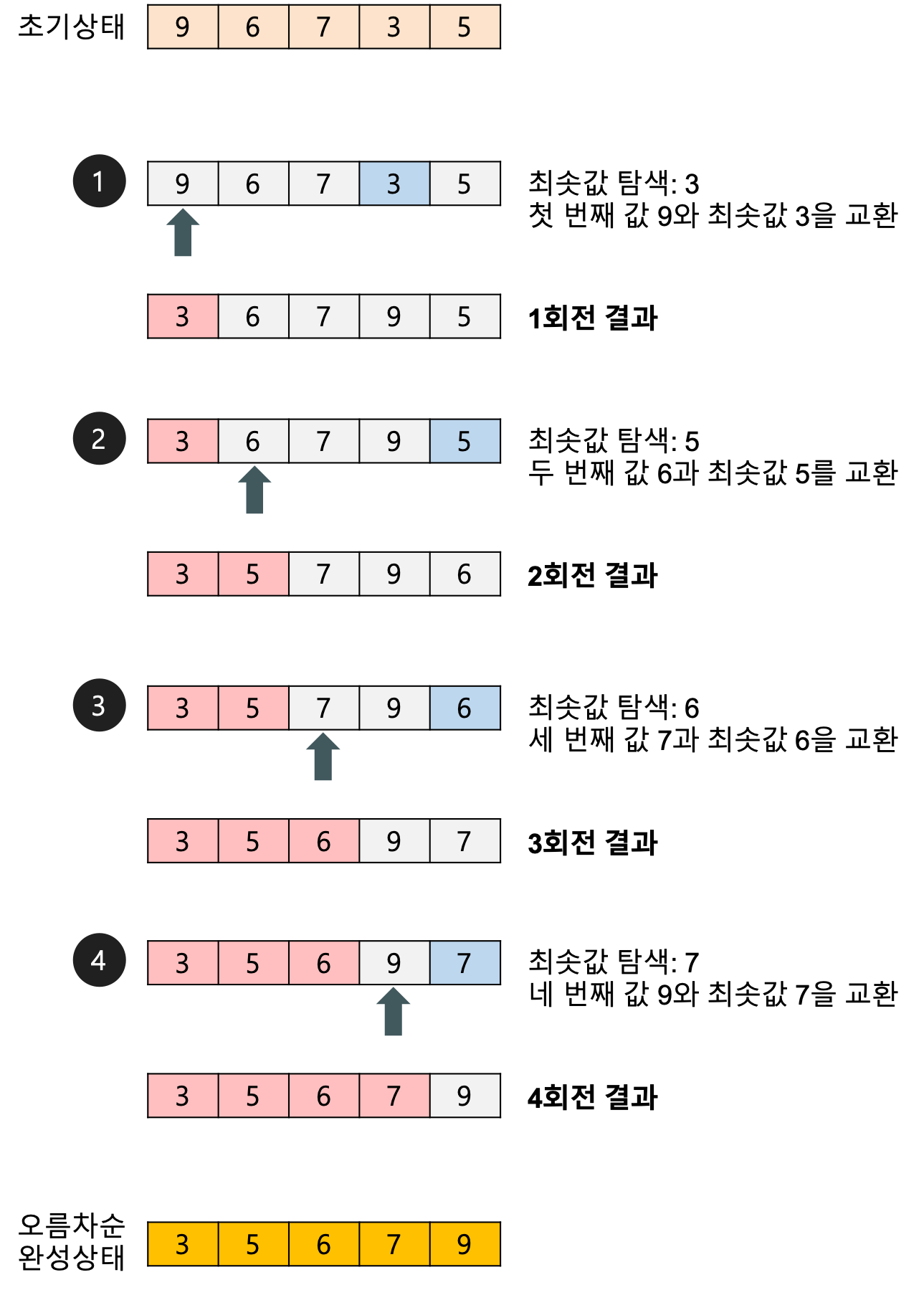
첫 번째 자료를 두 번째 자료부터 마지막 자료까지 차례대로 비교하여 가장 작은 값을 찾아 첫 번째로 놓고, 두 번째 자료를 세 번째 자료부터 마지막 자료까지와 차례대로 비교하여 그 중 가장 작은 값을 찾아 두 번째 위치에 놓는 과정을 반복하며 정렬을 수행한다.
예제
배열에 9, 6, 7, 3, 5가 저장되어 있다고 하고 오름차순으로 정렬할 때
예제 코드
void selectionSort(int arr[])
{
int n = arr.length;
for (int i = 0; i < n-1; i++)
{
int min_idx = i;
for (int j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
2. 버블 정렬 (Bubble Sort)
- 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
- 인접한 2개의 원소를 비교하여 크기가 순서에 맞지 않으면 교환한다.
- 시간복잡도 평균&최악 = O(n^2) 최상 = O(n) 공간복잡도 O(1)
정렬 과정
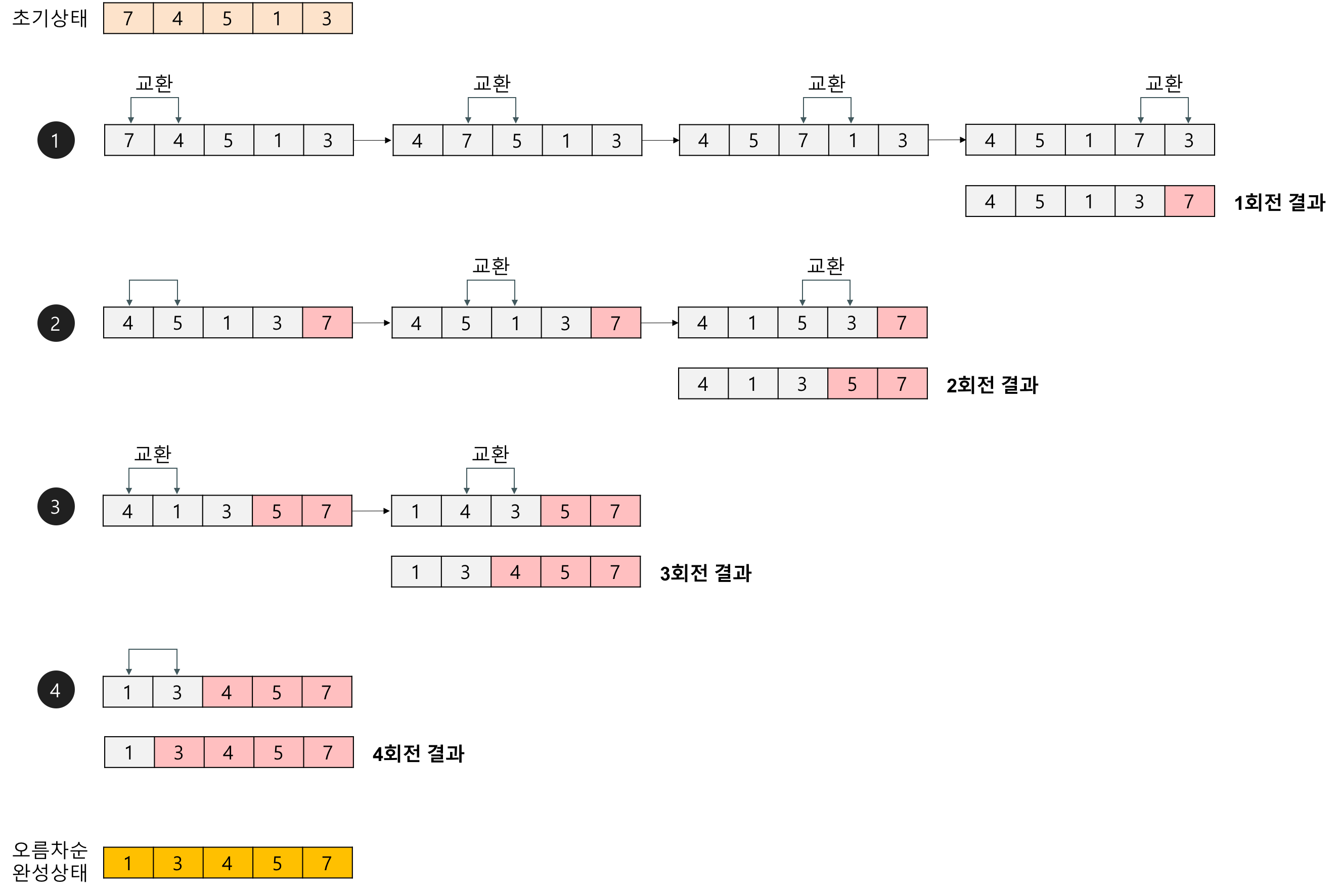
첫 번째 자료와 두번째 자료, 두번째 자료와 세번째 자료, 세번째와 네번째.. 이런 식으로 마지막 자료까지 비교하여 교환하면서 자료를 정렬한다.
배열의 끝까지 1회전을 실행하면 가장 큰 자료가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 자료가 제외된다. 이런식으로 원소의 개수만큼 회전을 실시하면 정렬이 되는 방식이다.
예제
배열에 7, 4, 5, 1, 3이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬할 때
예제 코드
static void bubbleSort(int[] arr) {
int n = arr.length;
int temp = 0;
for(int i=0; i < n; i++){
for(int j=1; j < (n-i); j++){
if(arr[j-1] > arr[j]){
temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
}
}
}3. 삽입 정렬 (Insertion Sort)
- 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘
- 매 순서마다 해당 원소를 삽입할 수 있는 위치를 찾아 해당 위치에 넣는다.
- 시간복잡도 최상 n, 평균, 최악 n^2 공간복잡도 O(1)
정렬 과정
삽입 정렬은 두번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬한다.
두번째 자료는 첫번째 자료, 세번째 자료는 두번째와 첫번째 자료, 네번째자료는 세번째, 두번째, 첫번째 자료와 비교한 후 자료가 삽입될 위치를 찾는다. 자료가 삽입될 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한칸씩 뒤로 이동시킨다.
처음 Key 값은 두번째 자료부터 시작한다.
예제
배열에 8, 5, 6, 2, 4가 저장되어 있다고 하고 오름차순으로 정렬할 때

예제 코드
void insertionSort(int arr[])
{
int n = arr.length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
4. 합병 정렬 (Merge Sort)
- 안정 정렬에 속하고, 분할 정복 알고리즘의 하나
- 분할 정복
- 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 방법
- 분할 정복 방법은 대개 재귀를 이용하여 구현한다.
- 시간복잡도 언제나 O(n x log n) 공간복잡도 O(n)
정렬 과정
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다.
- 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 길이가 0 또는 1이 될때까지 나눈다.
- 각 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. => 실제로 정렬이 이루어지는 시점
- 합병할때는 2개의 리스트의 값들을 처음부터 하나씩 비교하여 더 작은 값들을 새로운 sorted 리스트로 옮긴다.
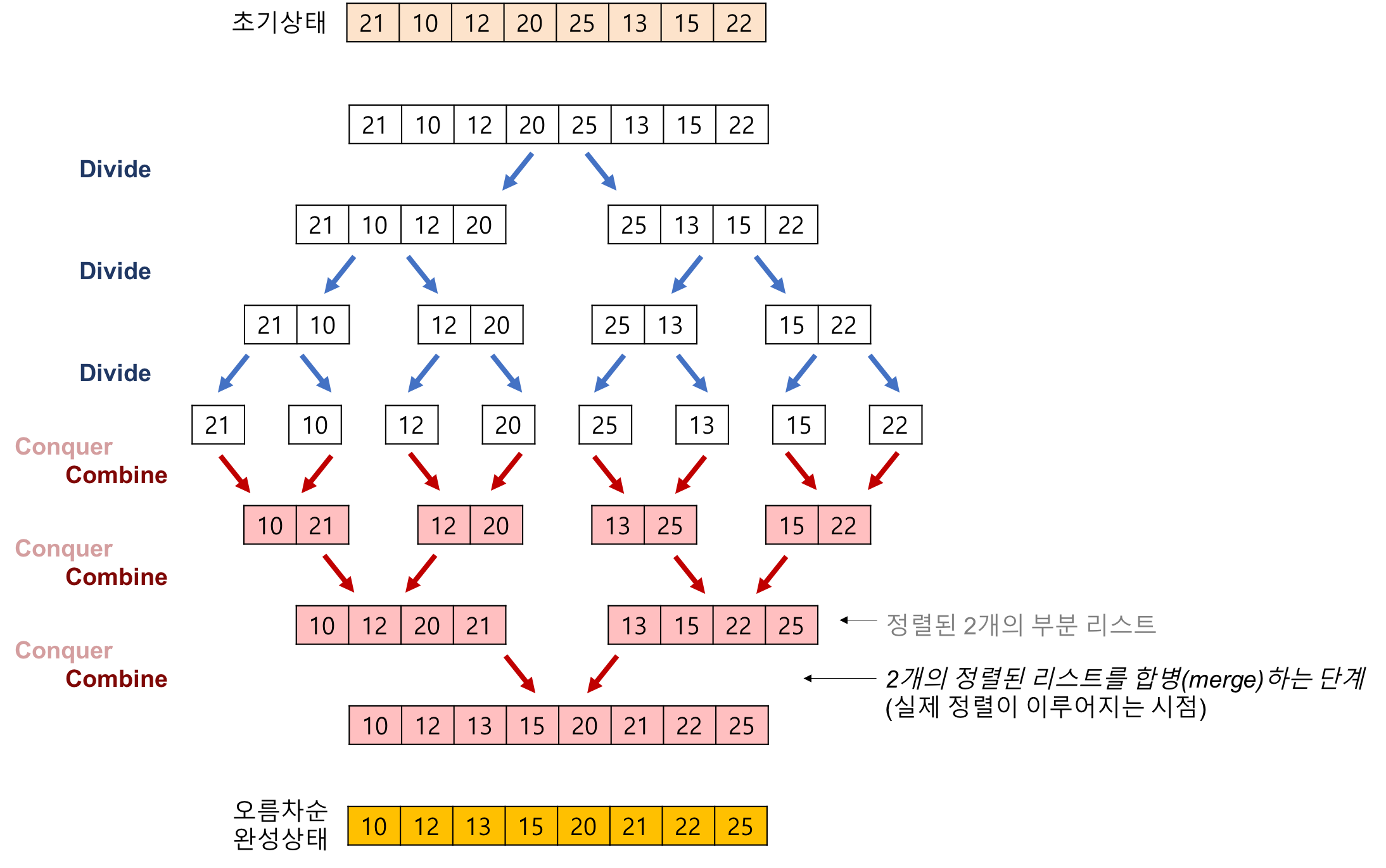
예제
배열에 27, 10, 12, 20, 25, 13, 15, 22가 저장되어 있다고 하고 오름차순으로 정렬할 때

예제 코드
void merge(int arr[], int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
int L[] = new int[n1];
int R[] = new int[n2];
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
int i = 0, j = 0;
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void sort(int arr[], int l, int r)
{
if (l < r) {
int m =l+ (r-l)/2;
sort(arr, l, m);
sort(arr, m + 1, r);
merge(arr, l, m, r);
}
}5. 힙 정렬 (Heap Sort)
- 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법
- 내림차순 정렬을 위해선 최대 힙, 오름차순 정렬을 위해선 최소 힙을 사용
- 시간복잡도 항상 O(nlog2n) 공간복잡도 O(1)
정렬 과정
- 정렬해야할 요소들로 최대 힙 or 최소 힙을 만든다.
- 하나씩 요소를 힙에서 pop해서 배열에 저장한다.
예제 코드
Java의 PriorityQueue를 이용하면 쉽게 Heap Sort 를 구현할 수 있다.
public static int[] heapSort(int[] arr) {
int n = arr.length;
int[] newArr = new int[n];
int index = 0;
PriorityQueue<Integer> q = new PriorityQueue<Integer>(n);
for(int i = 0; i < n; i++) {
q.add(arr[i]);
}
while(!q.isEmpty()) {
newArr[index] = q.poll();
index++;
}
return newArr;
}
그래도 Heap 자체 구현해서 해보자
heapSort 메서드
public static int[] heapSort(int[] arr) {
int n = arr.length;
int[] newArr = new int[n];
int index = 0;
Heap heap = new Heap();
for(int i = 0; i < n; i++) {
heap.insert(arr[i]);
}
int r;
while((r=heap.pop()) != -1) {
newArr[index] = r;
index++;
}
return newArr;
}
Node class
package sort;
public class Node {
int value;
Node left;
Node right;
Node parent;
public Node(int value,Node parent) {
this.value = value;
this.left = null;
this.right = null;
this.parent = parent;
}
}
Heap class
package sort;
import java.util.LinkedList;
import java.util.Queue;
public class Heap {
Node root = null;
public void insert(int value) {
if(root == null) {
root = new Node(value,null);
return;
}
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while(!queue.isEmpty()) {
Node n = queue.poll();
if(n.left == null) {
n.left = new Node(value,n);
if(n.value > n.left.value) {
n = n.left;
heapifyUp(n);
}
return;
} else {
queue.add(n.left);
}
if (n.right == null) {
n.right = new Node(value,n);
if(n.value > n.right.value) {
n = n.right;
heapifyUp(n);
}
return;
} else {
queue.add(n.right);
}
}
}
private void heapifyUp(Node n) {
while (n.parent != null && n.value < n.parent.value) {
int temp = n.parent.value;
n.parent.value = n.value;
n.value = temp;
n = n.parent;
}
}
// pop: 최소값을 제거하고 힙 재구성
public int pop() {
if (root == null) {
return -1;
}
int minValue = root.value;
// 마지막 노드를 찾기 위해 BFS
Queue<Node> queue = new LinkedList<>();
queue.add(root);
Node lastNode = null;
while (!queue.isEmpty()) {
lastNode = queue.poll();
if (lastNode.left != null) queue.add(lastNode.left);
if (lastNode.right != null) queue.add(lastNode.right);
}
// 루트 값을 마지막 노드 값으로 대체하고 마지막 노드 삭제
root.value = lastNode.value;
if (lastNode.parent != null) {
if (lastNode.parent.left == lastNode) {
lastNode.parent.left = null;
} else {
lastNode.parent.right = null;
}
} else {
root = null; // 트리에 노드가 하나만 있는 경우
}
// 힙 재구성
heapifyDown(root);
return minValue;
}
// 힙 재구성 (삭제 후 아래로 내리는 작업)
private void heapifyDown(Node n) {
while (n != null) {
Node smallest = n;
if (n.left != null && n.left.value < smallest.value) {
smallest = n.left;
}
if (n.right != null && n.right.value < smallest.value) {
smallest = n.right;
}
if (smallest != n) {
int temp = n.value;
n.value = smallest.value;
smallest.value = temp;
n = smallest;
} else {
break;
}
}
}
}
6. 퀵 정렬 (Quick Sort)
- 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다.
- 분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 정렬 속도를 자랑함.
- 합병 정렬과 달리 퀵 정렬은 리스트를 비균등하게 분할한다.
- 시간복잡도 O(nlog2 n) 공간복잡도 O(log n)
- 근데 이미 정렬된 리스트에 대해서는 오히려 느리다.
정렬 과정
- 리스트 안에 있는 한 요소를 선택한다. 이 요소를 피벗(pivot)이라고 한다.
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다.
- 이 과정이 끝나면 적어도 pivot은 정렬된 위치를 찾아가기때문에 순환호출이 반드시 끝나는 것을 보장한다.
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복 -> 리스트의 크기가 0이나 1이 될 때까지
예제
배열에5, 3, 8, 4, 9, 1, 6, 2, 7이 저장되어 있다고 하고 오름차순으로 정렬할 때

예제 코드
public static void quickSort(int[] arr, int s, int e) {
if (s >= e) return;
int pivot = arr[s];
int i = s + 1;
int j = e;
while (i <= j) {
while (i <= e && arr[i] <= pivot) {
i++;
}
while (j > s && arr[j] > pivot) {
j--;
}
if (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
arr[s] = arr[j];
arr[j] = pivot;
printArray(arr);
quickSort(arr, s, j - 1);
quickSort(arr, j + 1, e);
}
7. 셸 정렬 (Shell Sort)
- 삽입 정렬을 보완한 알고리즘
- 삽입 정렬은 어느 정도 정렬된 배열에 대해서는 대단히 빠르다
- 삽입 정렬의 문제점: 요소들이 삽입될 때, 이웃한 위치로만 이동
- 만약 삽입되어야 할 위치가 현재 위치에서 멀리 떨어진 곳이라면 많은 이동을 해야만한다.
- 시간복잡도 최상 n 최악 n^2 평균 n^1.5 공간복잡도 O(1)
정렬 과정
- 먼저 정렬해야 할 리스트를 일정한 기준 (간격)에 따라 분류
- 연속적이지 않은 여러 개의 부분 리스트를 생성
- 각 부분 리스트를 삽입 정렬을 이용하여 정렬
- 모든 부분 리스트가 정렬되면 다시 전체 리스트를 더 적은 간격의 부분 리스트로 만든 후에 알고리즘을 반복
- 위의 과정을 부분 리스트의 간격아 1이 될 때까지 반복
예제
배열에 10, 8, 6, 20, 4, 3, 22, 1, 0, 15, 16이 저장되어 있다고 하고 오름차순으로 정렬할 때

예제 코드
public static void shellSort(int[] arr) {
int n = arr.length;
// 초기 gap 설정: 배열 길이의 절반으로 시작하고, 매 단계마다 반으로 줄임
for (int gap = n / 2; gap > 0; gap /= 2) {
// gap 크기만큼의 간격을 두고 배열 요소를 비교하며 정렬
for (int i = gap; i < n; i += 1) {
int temp = arr[i]; // 현재 요소를 임시 저장
int j;
// gap만큼 떨어진 요소와 비교하며 위치를 조정
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
arr[j] = arr[j - gap]; // 크기가 더 큰 요소를 오른쪽으로 이동
}
arr[j] = temp; // 임시 저장된 요소를 올바른 위치에 삽입
}
// 각 gap 단계가 끝날 때 배열 상태를 출력 (디버깅 용도)
printArray(arr);
}
}

단순하지만 비효율적인 방법
- 삽입정렬
- 선택정렬
- 버블정렬
복잡하지만 효율적인 방법
- 퀵정렬
- 힙정렬
- 합병정렬
참고
https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
'알고리즘공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 벨만포드 (0) | 2025.01.24 |
|---|---|
| [알고리즘] 플로이드 워셜 (0) | 2025.01.24 |
| [알고리즘] 다익스트라 (0) | 2025.01.24 |
| [알고리즘] 최단 경로 찾기 (0) | 2025.01.20 |
| 1. 알고리즘이란 (0) | 2024.11.24 |


