플로이드워셜 (Floyd-Warshall) 알고리즘이란??
그래프의 모든 정점에서 다른 모든 정점까지의 최단거리를 각각 구하는 알고리즘
한 점에서 이웃 노드를 탐색하며 최단 거리를 구하는 다익스트라와 다르게 거쳐가는 중간 노드를 기준으로 최단 거리를 구한다.
음수가중치가 허용 되지만, 음수 사이클이 있으면 안된다.

우측의 경우는 2 -> 3 -> 2 사이클을 돌 때마다, 최단경로가 1씩 단축이 되어버리므로 이러한 음수 사이클이 있는 그래프에서는
플로이드 워셜을 사용할 수 없다.
또한 플로이드 워셜을 동적계획법을 이용하므로, 동적계획법의 개념을 잘 이해하는 것이 좋다.
시간복잡도
플로이드 워셜은 3중 반복문을 사용하기때문에 O(n^3)의 시간복잡도를 가진다. n은 정점의 개수
공간복잡도
path table을 만들때 N*N 크기의 2차원 배열을 생성하기때문에 O(n^2)의 공간복잡도를 가진다.
따라서 정점이 많은 경우, 음수 사이클이 없을 때 사용하면 될 것 같다.
구현 방식
- 2차원 배열 path 를 각 정점 사이의 가중치로 초기화한다. 가중치가 없는 경우 INF로 설정한다.
- 코드상으로 무한을 표시할 수 없으므로 대개 자료형의 가장 큰 값으로 설정 ex) Integer.MAX_VALUE
- 각 중간 정점 k에 대하여 시작 정점 i와 끝 정점 j의 가능한 모든 조합을 반복문으로 탐색한다.
- 현재 거리 (path[i][j]) 가 중간 정점 k를 거친 거리 (path[i][k] + path[k][j]) 보다 크면 2차원 배열을 업데이트한다.
- 모든 정점에 대해 2, 3 단계를 반복한다.
예제

예제 코드
플로이드워셜 알고리즘
package Path;
public class Floyd {
public static final int INF = Integer.MAX_VALUE;
private int[][] table;
private void setTable(int v, int[][] edges) {
table = new int[v][v];
for(int i = 0; i < v; i++) {
for(int j = 0; j < v; j++) {
if(i == j) {
table[i][j] = 0;
}
else {
table[i][j] = INF;
}
}
}
for(int i = 0; i < edges.length;i++) {
int a = edges[i][0] - 1;
int b = edges[i][1] - 1;
int cost = edges[i][2];
table[a][b] = cost;
table[b][a] = cost; // 무방향 그래프
}
}
public void findPath(int v, int[][] edges) {
setTable(v, edges);
for (int k = 0; k < v; k++) {
for (int i = 0; i < v; i++) {
for (int j = 0; j < v; j++) {
if (table[i][k] != Integer.MAX_VALUE && table[k][j] != Integer.MAX_VALUE) {
table[i][j] = Math.min(table[i][j], table[i][k] + table[k][j]);
}
}
}
}
printTable();
}
public void printTable() {
for (int i = 0; i < table.length; i++) {
for (int j = 0; j < table[i].length; j++) {
System.out.print(table[i][j] + " ");
}
System.out.println();
}
}
}
메인
package Path;
public class Main {
public static void main(String[] args) {
int vertex = 6; // 정점의 개수
int start = 0; // 시작 노드의 번호
int[][] edge = {{4, 1, 10}, {3, 5, 24}, {5, 6, 2}, // 간선들의 정보
{3, 1, 41}, {5, 1, 24}, {4, 6, 50},
{2, 4, 66}, {2, 3, 22}, {1, 6, 25}};
Floyd floyd = new Floyd();
floyd.findPath(vertex,edge);
}
}
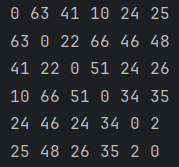
실행화면
'알고리즘공부' 카테고리의 다른 글
| [알고리즘] 벨만포드 (0) | 2025.01.24 |
|---|---|
| [알고리즘] 다익스트라 (0) | 2025.01.24 |
| [알고리즘] 정렬 (2) | 2025.01.22 |
| [자료구조] Heap (힙) (0) | 2025.01.21 |
| [자료구조] 그래프, dfs, bfs (0) | 2025.01.21 |
