다익스트라 알고리즘이란??
그래프의 한 정점에서 다른 모든 정점까지의 최단거리를 각각 구하는 알고리즘
그래프 방향의 유무와 구현 방법에 구애받지 않고 적은 비용으로 가장 빠르게 해답에 도달하는 최단경로 알고리즘이다.
하지만 음수 가중치가 존재한다면 사용할 수 없다.
정상 동작하는 경우도 있는데 음수 사이클이 있으면 잘못 나올 수도 있다.
그래서 웬만하면 음수 가중치가 없을 때만 사용하는 것이 좋을 것 같다. 음수 사이클이 있는지 판별도 안된다
음수가중치가 있다면 벨만포드를 사용하는 것을 추천한다.
다익스트라 알고리즘을 확장시킨 알고리즘인 A* 알고리즘도 존재한다.
구현 방식
1. 출발점으로부터 최단거리를 저장할 배열 - dist - 을 만들고, 출발 노드에는 0, 다른 노드들에게는 INF값을 채워 넣는다.
- 코드상으로 무한을 지정할 순 없기에 보통 해당 자료의 최대값을 설정한다. ex) Integer.MAX_VALUE
2. 현재 노드를 나타내는 변수 A에 출발 노드의 번호를 저장한다.
3. A로부터 갈 수 있는 모든 이웃 노드 B에 대해서 dist[A] + dist[A][B] 와 dist[B]의 값을 비교한다.
4. dist[A] + dist[A][B] 의 값이 더 작으면 dist[B]를 갱신한다.
5. A의 방문 상태를 방문 완료로 바꾼 후, A는 더 이상 사용하지 않는다.
6. 미방문 상태의 모든 노드들 중, 출발점으로부터의 거리가 제일 짧은 노드 하나를 골라서 그 노드를 A에 저장한다.
7. 도착 노드가 방문 완료 상태가 되거나, 더 이상 미방문 상태의 노드를 선택할 수 없을 때까지 위 과정을 반복한다.
이 작업을 마친 뒤, dist 배열의 도착 노드 index 값이 A 부터 도착 노드까지의 최단 거리가 된다. 만약 INF 값이라면 도달할 수 없다는 것이다.
7번 단계에서 거리가 가장 짧은 노드를 고르는 것이 시간복잡도에 영향을 많이 끼치게 되는데, 이때 우선순위 큐를 활용하면 이 비용을 줄일 수 있다.
예제
예를 들어 아래와 같은 정점이 8개인 그래프가 존재한다고 할때, 1번 정점부터 다른 정점들까지의 최단거리를 계산

1번 정점의 Cost는 0 다른 정점들은 INF로 초기화한다.

1번과 연결된 다른 모든 노드들과의 가중치를 보고 왼쪽 표를 아래처럼 업데이트 해준다.
.
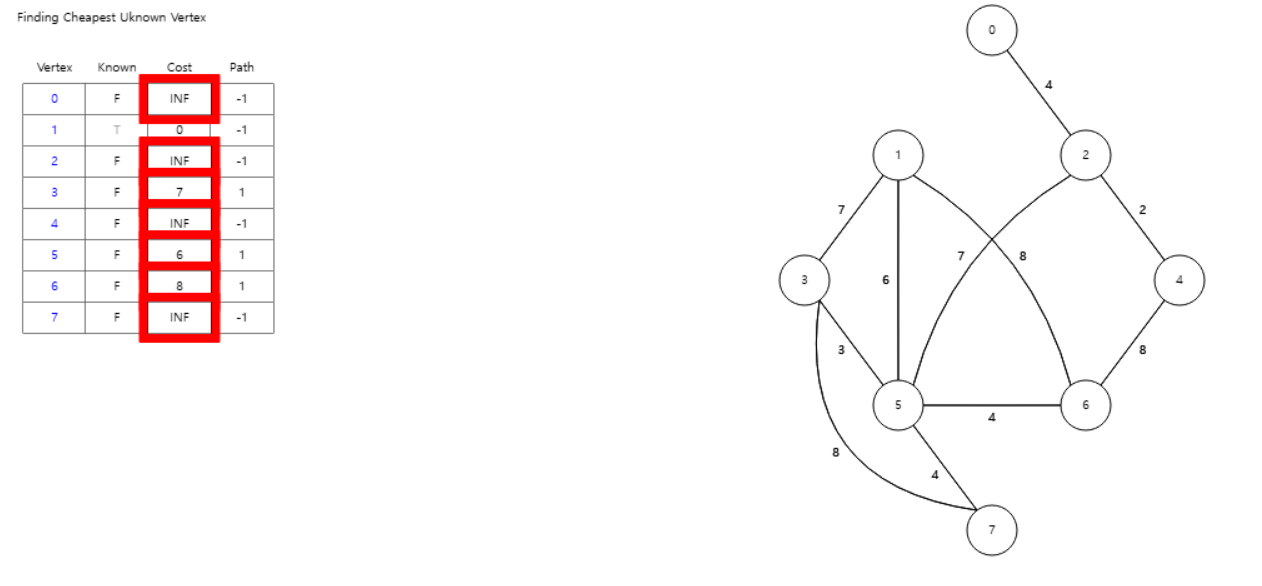
1을 방문처리하고
그 중에서 가장 작은 가중치를 가진 간선을 선택해 해당 노드로 이동한다. 예제에서는 5가 되겠다.

다시 5번에서 연결된 모든 노드와의 간선 가중치로 표를 업데이트한다.
그러나 이미 방문한 1번 노드의 값은 업데이트하지 않는다.

3번 노드는 이미 7 값이 들어있으므로 7과 6+3을 비교해서 작은값이 설정될 것이다.
나머지 노드들에 대해서도 반복해주면 아래와 같이 결과가 나온다.

이제 다시 왼쪽 표에서 가장 작은 cost를 가진 노드로 이동해 위 과정을 반복한다.
언제까지?? visit가 false인 노드중에 갈 수 있는게 없거나 목표 노드에 도착할때까지

모든 과정이 끝나면 1번 노드에서 다른 모든 노드까지의 최단거리가 정리된 표가 완성된다.
예를들어 cost[3]은 1번에서 3번까지 가는데 필요한 최저 비용인 것이다.
path라는 변수로 이전 노드까지 저장하면 경로까지 표시가 가능하다.
예제 코드
다익스트라 알고리즘
package Path;
import java.util.*;
public class Dijkstra {
HashMap<String,Integer> edges;
List<List<Integer>> graph;
private void setGraph(int v, int[][] edge) {
graph = new ArrayList<List<Integer>>();
edges = new HashMap<>();
for(int i = 0; i < v; i++) {
graph.add(new ArrayList<>());
}
for(int i = 0; i < edge.length; i++) {
int a = edge[i][0]-1;
int b = edge[i][1]-1;
graph.get(a).add(b);
graph.get(b).add(a);
String key = a + "-" + b;
String key2 = b + "-" + a;
edges.put(key,edge[i][2]);
edges.put(key2,edge[i][2]);
}
}
public int[] findPath(int v, int[][] edge, int start) {
setGraph(v, edge);
int[] costs = new int[v];
int[] path = new int[v];
boolean[] visited = new boolean[v];
Arrays.fill(costs, Integer.MAX_VALUE);
Arrays.fill(path, -1);
Arrays.fill(visited, false);
int s = start;
costs[s] = 0;
while(s != -1) {
List<Integer> list = graph.get(s);
visited[s] = true;
for(int i = 0; i < list.size(); i++) {
int u = list.get(i);
String key = u + "-" + s;
int value = edges.get(key);
if(!visited[u]) {
if(costs[u] > costs[s] + value) {
costs[u] = costs[s] + value;
path[u] = s;
}
}
}
int min = Integer.MAX_VALUE;
int min_index = -1;
for(int i = 0; i < costs.length; i++) {
if(!visited[i] && min > costs[i]) {
min = costs[i];
min_index = i;
}
}
s = min_index;
}
return costs;
}
}
메인
package Path;
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int vertex = 6; // 정점의 개수
int start = 0; // 시작 노드의 번호
int[][] edge = {{4, 1, 10}, {3, 5, 24}, {5, 6, 2}, // 간선들의 정보
{3, 1, 41}, {5, 1, 24}, {4, 6, 50},
{2, 4, 66}, {2, 3, 22}, {1, 6, 25}};
Dijkstra dijkstra = new Dijkstra();
int[] result = dijkstra.findPath(vertex,edge,start);
System.out.println(Arrays.toString(result));
}
}
실행 결과

'알고리즘공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 벨만포드 (0) | 2025.01.24 |
|---|---|
| [알고리즘] 플로이드 워셜 (0) | 2025.01.24 |
| [알고리즘] 정렬 (2) | 2025.01.22 |
| [알고리즘] 최단 경로 찾기 (0) | 2025.01.20 |
| 1. 알고리즘이란 (0) | 2024.11.24 |

